GEOMETRY SOLVED QUESTIONS 1

GEOMETRY QUESTIONS 1

 

1. An angle which is greater then 180° but less than 360° is called

A - Acute Angle

B - Obtuse Angle

C - Straight Angle

D - Reflex Angle

Answer - B

An angle that is greater than 180°  but less than 360° is called a reflex angle.

2. The complement of 62° is.

A - 118°

B - 28°

C - 38°

D - 48°

Answer - B

Explanation

Complement of 62°= (90° – 62°) = 28°.

3. The supplement of 60° is

A - 30°

B - 40°

C - 120°

D - 300°

Answer - B

Explanation

Supplement of 60° = (180°-60°) =120°.

4. The complement of 72° 40' is

A - 107°20'

B - 27°20'

C - 17°20'

D - 12°40'

Answer - C

Explanation

Complement of 72° 40' = (90°-72° 40') =17° 20'.

5. An angle is one-fifth of its supplement. The measure of the angle is

A - 15°

B - 30°

C - 75°

D - 150°

Answer - B

Explanation

x = 1/5 (180 – x )

⇒ 5x = 180 – x

⇒ 6x = 180

⇒ x = 30°.

6. If an angle is its own complementary angle, then its measure is

A - 30°

B - 45°

C - 60°

D - 90°

Answer - B

Explanation

x=(90-x)

⇒ 2x = 90

⇒ x = 45° .

7. How many angles are made by rays shown in the figure?

       

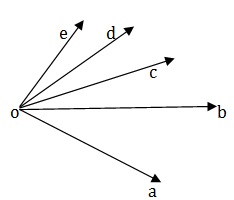
A - 5

B - 6

C - 8

D - 10

Answer - D

Explanation

The angle is ∠AOB, ∠BOC,∠COD,∠DOE,∠AOC,∠AOD, ∠AOE,∠BOD,∠BOD,∠COE.

Thus, 10 angles are formed.

8. An angle is 24° more than its complement. The measure of the angle is

A - 57°

B - 47°

C - 53°

D - 66°

Answer - A

Explanation

x – (90-x ) = 24

⇒ 2x = 114

⇒ x = 57

∴ The required angle is 57°.

9. An angle is 32° less than its supplement. The measure of the angle is

A - 37°

B - 74°

C - 48°

D - 66°

Answer - A

Explanation

(180 –X) – X = 32

⇒ 2x = 180 – 32 = 148

⇒ x = 74.

The required angle is 74°.

10. Two Supplementary angles are in the ratio 3:2. The smaller angle measures

A - 108°

B - 81°

C - 72°

D - 66°

Answer - C

Explanation

Let the measures of the angle be (3x)° and (2x)°. Then,

3x+2x=180

⇒ 5x = 180

⇒ x = 36.

Smaller angle = (2x)° = (2*36)° = 72°.

11. In the given figure, AOB is a straight line, ∠AOC = 68°, and ∠BOC = x°. The value of the x is

                    

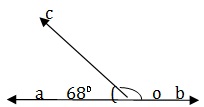
A - 120°

B - 22°

C - 112°

D - 132°

Answer - A

Explanation

Since ∠AOB is a straight angle, we have

X+ 68 = 180

⇒ x= (180-68)°  = 120°

12. In the given figure, AOB is a straight line, ∠AOC = (3x+20)° and ∠ BOC =(4x-36)°. The value of the x is

                                                 

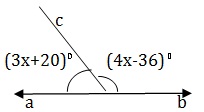
A - 32°

B - 22°

C - 26°

D - 24°

Answer - B

Explanation

Since ∠ AOB is a straight angle, we have

∠AOC + ∠ BOC  =180°

⇒ 3x + 20 +4x – 36 = 180

⇒ 7x = 164

⇒ x = 22.

13. In the given figure , AOB is a straight line, ∠ AOC = (3x-8)° and ∠COD =50 and ∠BOD° =(x+10)°. The value of the x is

                    

A - 32°

B - 42°

C - 36°

D - 52°

Answer - A

Explanation

Since ∠AOB is a straight angle , we have

∠AOC  + ∠ COB  + ∠ BOD  = 180°

⇒ (3X – 8)° + 50° + (X+ 10)° = 180°

⇒ 4X = 128

⇒ X = 32.

14. The angles of a triangle are in the ratio 2:3:7. The measure OF the smallest angle is:

A - 90⁰

B - 60⁰

C - 45⁰

D - 30⁰

Answer : D

Explanation

let the angles be (2x)⁰,(3x)⁰, and (7x)⁰. Then,

2x+3x+7x =180

⇒ 12x =180

⇒ x=15

Smallest angle = (2x)⁰ = 30⁰

15. If ∆ ABC is an isosceles triangle with ∠ C = 90⁰ and AC = 5cm , Then AB =?

A - 2.5 cm

B - 5 cm

C - 10cm

D - 5√2 cm

Answer : D

Explanation

Clearly BC =AC=5cm.

AB² = AC²+ BC² =5² +5²= 50

⇒ AB = √50 = 5√2 cm.

16.  The length of the longest rod which can fit into a cubical room of 5 m side is

A. 5.334 m

B. 12.11 m

C. 9.320 m

D. 8.440 m

E. 3.050 m

Sol: Option B

The length of the longest rod, which can fit into the cubical room, is √3 × side.

Hence the answer is √3 × 7 = 12.11m

17.  The measure of an angle which is five times its complement is

A. 26°

B. 75°

C. 78°

D. 18°

E. 122°

Sol: Option B

Let the angle be x.

∴ x = 5(90 – x)

⇒ x = 450 – 5x

⇒ 6x = 450

⇒ x = 750

18. If the breadth of a rectangle is decreased by 20 % and the length increased by 10 %, a square of area 1936 m2 is obtained. The area of the rectangle in square meters is

A. 2200

B. 3500

C. 2250

D. 1450

E. 4506

Sol: Option A

1.1L × 0.8B = 1936 ⇒ LB = 2200m².

∴ Area of rectangle = 2200m².

19. The height of a cylinder is 16 cm and the radius of the base is 6 cm. Find the area of the curved surface of the cylinder.

A. 480 sqcm

B. 560 sqcm

C. 603 sqcm

D. 720 sqcm0

E. 800 sqcm

Sol: Option C

The surface area = 2 πrh

= 2 π×6×16

= 603 sq.cm

20.  A cube of 600cm² surface area is melted to make x small cubes each of the 96mm² surface areas. X is

Sol : Surface area of larger cube = 600cm²

6L² = 600 L² = 100 L = 10cm.

volume of larger cube = 10 10 10 = 1000 cm² . Surface area of smaller cube = 100 mm² = 100/100

cm². 6l² = (100/100) ⇒ l² = (1/6)cm

Volume of smaller cube = 1/6 1/6 1/6

= (1/216)cm² .

x = 1000/1/216 = 216000

21. A copper sphere of diameter 36cm is drawn into a wire of diameter 8mm. Find the length of the wire.

Sol: In this case,4/3πR3 = πr2h where R is the radius of the sphere, r is the radius of the wire, and 'h' is the length of the wire.

Hence 4/3 (36/2)3 = (8/10.h/2)2

So h =48600cm

22.  The difference between the circumference & radius of a circle is 37 meters. Find its circumference.

Sol : 2πr - r =37 ⇒ r(2π - 1) = 37

(2× (22/7) - -) = 37 ⇒ r(37/7) =37 ⇒ r = 7

r ∴ 2πr-7 = 37 ⇒ 2πr = 44m.

23.  A vertical ladder of 20 m leaning straight against a wall casts a shadow of 10 m long on the ground. At the same time, a building casts a shadow 50 m long on the ground. find the height of the tower

A. 150m

B. 100m

C. 200m

D. 25m

Sol: When the length of the ladder =  20 m

then the length  of the shadow = 10 m i.e; in this case

length = 2 x shadow

With the same angle of inclination of the sun, the length of the tower that casts a shadow of 50 m will be

2 x 50 = 100 m

i. e; the height of the tower is 100 m

24. . All the angles of two isosceles triangles are equal but they a difference in their area. Their area is in the ratio 5:10. find the ratio of their corresponding heights?

A.3/2

B.4/5

C.5/4

D.2/3

Sol: (Ratio of corresponding heights)² = Ratio of area of similar triangles

Ratio of corresponding heights  in this question = √(16/25) = 4/5

25. Find the sum of squares of the medians of a triangle whose sides are 6 cm, 7 cm, 8 cm

A. 259.52 cm²

B. 111.75 cm²

C.256.84 cm²

D. 124.75cm²

Sol: 3 x (Sum of squares of the sides of the triangle) = 4 x (Sum of squares of the medians of the triangle)

(3/4) x (62 x 72 x 82) = Sum of square of the medians

= (3/4) x 149 = 111.75 cm²

26. . Find the area of a trapezium whose parallel sides are 20 cm and 18 cm long, and the distance between them is 15 cm.

A.225 cm²

B.275 cm²

C.285 cm²

D.315 cm²

Sol: Area of trapezium =1/2 ×(sum of parallel sides) ×(distance between them )

1/ 2 (20+18) x 15

=285 cm²

27. The sector of a circle has a radius of 21 cm and a central angle 135degree. Find its perimeter.

A.108 cm

B.93.5 cm

C.107 cm

D.92.5 cm

Sol:  Given: radius of circle=21 cm

Central angle=135°

To find the Perimeter of sector.

Firstly we have to find the length of the arc.

So length of arc = theta/ 360°×2pi R

= 135°/360°×2×22/7 × 21

= 27°/72° × 44×3

= 9°/24° × 44×3

= 9/6×44

= 3/2× 44

= 3 × 22= 66 cm

Now, Perimeter of sector= 2×r + length of arc

= 2×21+ 66

= 42+66

= 108 cm

28. Find the curved surface area of a cylinder of length 7 m and a base of radius 3 meters.

A. 112

B. 122

C. 132

D. 182

E. None of These

Correct Ans: 132

Explanation:

Let r and h be the radius and height of the cylinder respectively.
r = 3 and h = 7
Curved Surface area , CSA = 2 * pi * r * h CSA = 2 x (22/7) x 3 x 7 = 132 sq m

 

29. Find the length of the diagonal of a cuboid 12m long, 9m broad, and 8 m high.

  A. 18

  B. 17

  C. 20

  D. 29

   E. None of These

Correct Ans: 17

Let l, b and h be the length, breadth and height of the cuboid respectively.
Diagonal = sqrt(l*l + b*b + h*h) = sqrt(12 x 12 + 9 x 9 + 8 x 8) = sqrt(144+81+64) Diagonal = sqrt(289) = 17

30. Find the perimeter of the rectangle having length 24 cm and breadth 21 cm.

A. 504

B. 45

C. 95

D. 90

E. None of These

Correct Ans: 90

Given length of the rectangle, l = 24 cm Breadth of the rectangle, b= 21 cm Perimeter of the rectangle is, P = 2(l+b) P = 2 * (24 + 21) cm P = 2 x 45 = 90 cm

31. Find the curved surface area of a cylinder of length 7 m and a base of radius 4 meter.

A. 196

B. 156

C. 166

D. 176

E. None of These

Correct Ans: 176

Let r and h be the radius and height of the cylinder respectively. r = 4 and h = 7 Curved Surface area , CSA = 2 * pi * r * h CSA = 2 * (22/7) * 4 * 7 = 176 sq m

32. Area of the base of a cuboid 49 sq m, area of side face, and other side face are 64 sq m and 25 sq m respectively. Find the volume of the cuboid

A.  240

B.  260

C.  290

D.  280

E.  None of These

Correct Ans: 280

Let l, b, and h be the length, breadth, and height of the cuboid respectively. According to given data, Area of the base of a cuboid = l x b = 49 , ----> (1)

Area of the one side face = b x h = 64 ------> (2)

Area of the other side face = h x l = 25 -----> (3)

On multiplying the above equations we get l x b x b x h x l x h = 49 x 64 x 25

=> (l x b x h)² = 49 x 64 x 25

=> l x b x h = 7 x 8 x 5 = 280

Volume of the cuboid = l x b x h = 280

33. Find the curved surface area of a cylinder of length 7 m and a base of radius 3 meter.

 A. 122

 B. 112

 C. 132

 D. 142

 E. None of These

Correct Ans: 132

Let r and h be the radius and height of the cylinder respectively.
r = 3 and h = 7
Curved Surface area , CSA = 2 x pi x r x h CSA = 2 x (22/7) x 3 x 7 = 132 sq m

34. Find the length of the diagonal of a cuboid 10m long, 8 m broad, and 5 m high.

A. 13.75

               B. 14

               C. 17

               D. 23

               E. None of These

Correct Ans: 13.75

Let l, b and h be the length, breadth and height of the cuboid respectively.
Diagonal of cuboid = sqrt(lxl + bxb + hxh) = sqrt(10 x 10 + 5 x 5 + 8 x 8) = sqrt(100+25+64) Diagonal = sqrt(189) = 13.75

35. A tennis court has a length of 29 units, and breadth of 20 units. Find the area of the tennis court ?

 A. 841

 B. 49

 C. 290

 D. 580

 E. None of These

Correct Ans: 580

Area of Rectangle = length x breadth
29 x 20= 580

36. Find the volume of a cube of side 12 cm

A. 1788

 B. 1728

 C. 1628

 D. 1718

 E. None of these

Correct Ans: 1728

Let the side of the cube be a Then, Volume of the cube V = a^3 = a x a x a V = 12 x 12 x 12 = 1728 cu cm

37. Find the volume of the cylinder which has a height of 14 meters and a base of radius 3 meters. ?

 

A. 396

B. 386

C. 406

 D. 416

 E. None of these

Correct Ans: 396

Let r and h be the radius and height of the cylinder.
Volume, V = pi* r² * h V = (22/7) x 3 x 3 x 14 = 22 x 9 x 2 = 44 x 9 V = 396 cu m

38. Find the volume of a cuboid with dimension 22 cm by 12 cm by 7.5 cm

 A. 1960

 B. 1880

 C. 1980

 D. 1970

 E. None of these

Correct Ans:1980

Length of the cuboid be l, breadth of the cuboid be b, and height of the cuboid be h.
Volume of the cuboid is, V = l x b x h V = 22 x 12 x 7.5 = 1980 cu cm.

39. The circumference of a park is 750 m. A and B start walking from the same direction at 6.75 kmph and 4.75 kmph. At what time will they meet each other again?

 A. 3 hours

 B. 2.5 hours

 C. 3.5 hours

 D. 4 hours

 E. None of These

Correct Ans:3 hours

Time taken by A to complete one revolution= 750/(6.75 x 5)/18 sec = (750*18)/(6.75*5)sec.
Time taken by B = (750 x 18)/(4.75 x 5) sec
Time required = LCM of numerators / HCF of denominators = 750 x 1800 / 125 = 1800 x 6 seconds = (1800 x 6)/3600 hrs = 3 hours

40. Length and breadth of a rectangular plot is 20m & 27m respectively. Find the Difference between Area and Perimeter ?

A. 493

 B. 352

 C. 540

 D. 446

 E. None of These

Correct Ans: 446

Difference between area & perimeter = (length x breadth ) - (2 x (length + breadth) ) = (20 * 27 ) - (2 * (20 + 27) ) = 540 - (2 * 47) = 540 - 94 = 446

41. Steve walks diagonally in a Square shaped park. Steve covers a distance of 10m. Can you find the area of the Square park ?

 A. 100sq.m

 B. 25sq.m

 C. 141.42sq.m

 D. 50sq.m

 E. None of These

Correct Ans: 50sq.m

Given Steve walks distance of 10m
Park is in the shape of Square, so the area of the park (in the shape of Square) = (Diagonal²) / 2
=> (10²)/2 = 50sq.m

42. The area of a rhombus is 256 square cm and one of its diagonal is twice the other in length. Then length of its larger diagonal is?

 A. 32 cm

 B. 16 cm

 C. 48 cm

 D. 24 cm

 E. None of These

Correct Ans: 32 cm

Let diagonal of Rhombus be d1 = x
Second diagonal = d1 * 2 = 2x cm
Area of rhombus = 1/2 d1 .d2

=>1/2 d1 .d2 = 256

=>1/2 * x * 2x = 256

=> x² = 256

=>x = √256 = 16 cm
Larger diagonal = 2x

=>2 * 16 = 32cm

43. Diameter of a roller is 2.4 m and it is 1.68 m long. If it takes 1000 complete revolutions once over to level a field, then the area of the field is ?

A. 12672 sq m

 B. 12671 sq m

 C. 12762 sq m

 D. 11768 sq m

 E. None of These

Correct Ans: 12672 sq m

Given, Diameter of roller = 2.4 m

=> radius = 2.4 / 2 = 1.2 m
Circumference = 2Π x r = 2Π x1.2 m
Area covered in one revolution = 2.4 Π x 1.68 = 12.672 sq m ;
Total area of the field = 12.672 x 1000 = 12672 sq. m

44. If the perimeter of a rectangle is 180 m and the difference between the length and the breadth is 8 meters, what is the area of the rectangle?

 A. 2116 sq m

 B. 2047 sq m

 C. 2090 sq m

 D. 2009 sq m

 E. None of These

Correct Ans: 2009 sq m

Let x = length of the rectangle and breadth = (x – 8) m
Given , perimeter of the rectangle = 180 m perimeter of the rectangle = 2 * (l+b)

=> 2(x + x - 8)= 180

=> (2x - 8) = 90

=>2x = 90 + 8 = 98

=> x = 49 m
Breadth = 49 – 8 = 41 m
Area of the rectangle = l * b = 49 x 41 = 2009 sq. m

45. The side of a square is 2 cms less than the length of a rectangle and the breadth of the rectangle is 5 cms less than the side of the square. The area of the square is 324 sq. cms. What is the area of the rectangle?

 A. 250 sq. cms

 B. 260 sq. cms

 C. 254 sq. cms

 D. 258 sq. cms

 E. None of These

Correct Ans: 260 sq. cms

Side of a square = ?Area = ?324 = 18 cm
Length of the rectangle = 18 + 2 = 20 cm and breadth = 18 – 5 = 13 cm
Area of rectangle = Length x breadth = 20 x 13 = 260 sq. cm

46. One of the angles of a right angled triangle is 15°, and the hypotenuse is 1 m. The area of the triangle (in square cm) is

 A. 1220

 B. 1200

 C. 1250

 D. 1215

 E. None of These

Correct Ans: 1250

Sin 15° = sin (45° – 30°) = sin 45° x cos 30° – cos 45° x sin 30°
=1/√2 x √3/2 – 1/√2 x 1/2
= √3/2√2 – 1/2√2
= (√3 - 1) / 2√2

cos 15° = cos (45° – 30°) = cos 45°. cos 30° + sin 45°. sin 30°
= 1/√2 x√3/2 + 1/√2 x 1/2
=√3/2√2 + 1/2√2
= (√3+1)/2√2;

Let ABC be the right-angled triangle
AB = AC sin 15°
= (√3 – 1)/2√2 m

BC =AC cos 15° = (√3+1)/2√2 m

Area of ABC = 1/2 x AB x BC
= (1/2 x (√3 - 1)/ 2√2 x (√3+1)/ 2√2) sq m
= (3 - 1)/16 sq m
= 1/8 sq m
= 10000/8 cm
= 1250 sq cm

47. An equilateral triangle and a regular hexagon have equal perimeters. The ratio of the area of the triangle and that of the hexagon is ?

 A. 1:1

 B. 2:3

 C. 3:2

 D. 3:4

 E. None of These

Correct Ans: 2:3

Let x = side of triangle and y = side of regular hexagon
Given, 3x = 6y 

=> x = 2y 
Area of triangle = (3/4) x²
=> Area of hexagon = 6 X (3/4) y² 

=> 6 X (3/4) * (x² /4)  

Substituting y = x/2

=> 3 (3/8) x²
=> Required ratio = (3/4) x² : 3 (3/8) x² = 2 : 3

48. Area of the base of a cuboid 9 sq m, area of side face and other side face are 16 sq m and 25 sq m respectively. Find the volume of the cuboid ?

 A. 60

 B. 120

 C. 240

 D. 360

 E. None of These

Correct Ans:60

Let l, b, and h be the length, breadth, and height of the cuboid respectively.

Given, Area of the base of a cuboid = l x b = 9 ,
Area of the side face = b x h = 16
Area of the other side face = h x l = 25

On multiplying the above equations we get
l x b x b x h x l x h = 9 x 16 x 25
(l x b x h)² = 9 x 16 x 25
l x b x h = 3 x 4 x 5 = 60

Volume of the cuboid = l x b x h = 60

49. Find the area of the parallelogram whose length and breadth are 12 cm and 15 cm respectively.

 A. 90 sq cm

 B. 180 sq cm

 C. 144 sq cm

 D. 225 sq cm

 E. None of These

Correct Ans:180 sq cm

Area of the parallelogram = l x b Area = 12 x 15 = 180 sq cm

50. The length and breadth of a rectangular plot is 25m & 34m respectively. Find the Difference between Area and Perimeter?

 A. 791

 B. 614

 C. 850

 D. 732

 E. None of These

Correct Ans:732

Difference between area & perimeter of rectangle = (length x breadth ) - (2 x (length + breadth) ) = (25 * 34 ) - (2 * (25 + 34)) = 850 - ( 2 * 59) = 850 - 118 = 732