GEOMETRY

GEOMETRY

1. Basics of Geometry:

• Line Segment

            

The straight path between two points A and B is called a line segment AB. A line segment has two endpoints.

•  Ray

             

On extending a line segment AB indefinitely in one direction we get the ray AB. Ray AB has one endpoint, namely A.

 

2. Lines and Angles

• LINE

             

   A line segment AB extended indefinitely in both directions is called line AB.

--A line contains infinitely many points.

 --Through a given point, infinitely many lines can be drawn.

 --One and only one line can be drawn to pass through two given points A and B.

 --Two-line meet in a point.

 --Two planes meet in a line.

•  Collinear

            

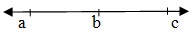
In the given figure, the points A, B, C are collinear.

• Concurrent Lines

Three or more lines intersecting at the same points are called concurrent lines.

•  Angle

              

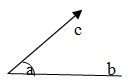
Two rays OA and OB having a common endpoints O form angle AOB, written as ∠AOB

•  Measure of an Angle

The amount of turning from OA to OB is called the measure of ∠AOB written as m(∠AOB).

•  An angle of 360°

If a ray OA starting from its original position OA, rotates about O in an anticlockwise direction and after a complete rotation comes back to its original position, then we say that it has rotated through 360. This complete rotation is divided into 360° equal parts. Then, each part is called 1 degree, written as 1°

 1° = 60 minutes, written as 60'

 1 minute = 60 seconds, written as 60"

 3. Types of Angle:

 --Right angle - An angle whose measure is 90° is called a right angle.

 --Acute angle - An angle whose measure is less than 90° is called an acute angle.

 --Obtuse angle - An angle whose measure is more than 90° but less than 180°, is called an obtuse angle.

 ---Straight angle - An angle whose measure is 180° is called a Straight angle.

 --Reflex angle - An angle whose measure is more than 180° but less than 360°, is called a Reflex angle.

 ---Complete angle - An angle whose measure is 360°, is called a complete angle.

 ---Equal angle - Two angles are said to be equal if they have the same measure.

 ---Complementary angle - Two angles are said to be complementary if the sum of their measures is 90. For example, angles measuring 65° and 25° are complementary angles.

 ---Supplementary angle - Two angles are said to be supplementary if the sum of their measures is 180°. For example, angles measures 70° and 110° are supplementary.

 ---Adjacent angle - Two angles are called adjacent angles if they have the same vertex and a common arm such that non-common arms are on either side of the common arm. In the given figure, ∠AOC and ∠BOC are adjacent angles.

 ---Vertically Opposite Angles

If two lines A Band CD intersect at a point O, then AOC, BOD, and BOC, AOD is two pair of vertically opposites

Vertically opposite angles are always equal.

 

4. Important points:

 --If a ray stands on a line, then the sum of two adjacent angles so formed is 180° In the given figure, ray CP stands on line AB.

       

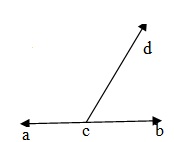
∴ ∠ACD + ∠BCD = 180°.

 ---The sum of all angles formed on the same side of a line at a given point on the line is 180°. In the given figure four angles are formed on the same side of AOB.

       

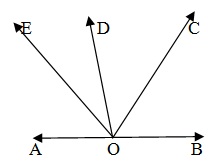
∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.

 ---The sum of all angles around a point is 360° In the given figure five angles are formed around a point O.

      

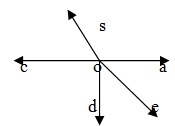
∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°

 

5. Parallel lines:

 If two lines lie in the same plane and do not intersect when produced on either side then such lines are said to be paralleled and we write, L||m.

 ---Traversal line cutting parallel lines

       

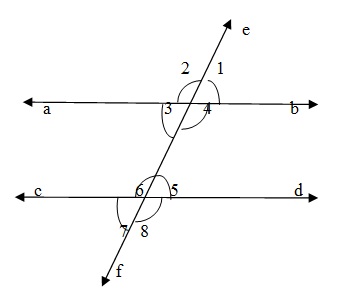
Let two parallel lines AB and CD be cut by a transversal EF. Then

Corresponding angle are equal

 (∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)

Alternate interior angles are equal.

 (∠3 =∠5 )  and  (∠4 =∠6 )

Consecutive interior angles are supplementary

 ∠4+∠5 = 180° and ∠3 +∠6 = 180

 

6. Triangle:

           

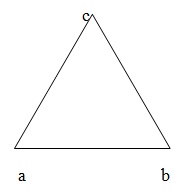
A figure bounded by three straight lines is called a triangle. In the given figure, we have ∆ABC; ∆ABC having three vertices A, B, C. In has three angles, namely ∠A,∠B, and ∠C. It has three sides, namely AB, AC, and BC.

 

• Types of Triangle

 A triangle having all sides equal is called an equilateral triangle.

 A triangle having two sides equal is called an isosceles triangle.

 A triangle having all sides of different lengths is called a scalene triangle.

 A triangle one of whose angles measures 90°, is called a right triangle.

 A triangle one of whose angle lies between 90° and 180° is called an obtuse triangle.

 A triangle each of whose angles is acute is called an acute triangle.

 The sum of all sides of a triangle is called the perimeter of the triangle.

 The sum of two sides of a triangle is greater than the third side.

 In a right-angled ABC in which ∠B = 90°, we have AC² =AB²+BC². This is called Pythagoras Theorem.

 

7.Quadrilateral:

 A figure bounded by four straight lines is called a quadrilateral. The sum of all angles of a quadrilateral is 360°.

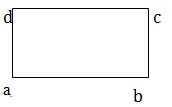
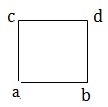
•  Rectangle - A quadrilateral is called a rectangle if its opposite side is equal and each of its angles is 90°. In given fig. ABCD is a rectangle.

                  

•  Square - A quadrilateral is called a square if all of its sides are equal and each of its angles measures 90°. In given fig. ABCD is square in which AB = BC = CD = DA.

                         

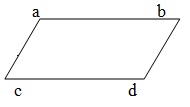
•  Parallelogram - A quadrilateral is called a parallelogram if its opposite sides are parallel. In given fig. ABCD is a parallelogram in which AB = DC & AD = BC.

                               

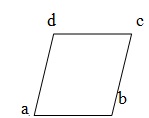
•  Rhombus - A parallelogram having all sides equal is called a rhombus. In given fig. ABCD is a rhombus in which AB =BC =CD=DA, AB || DC and AD || BC.

                               

 Important Facts

A quadrilateral is a rectangle if opposite sides are equal and its diagonals are equal.

 A quadrilateral is a Square if all sides are equal and the diagonal are equal.

 A quadrilateral is a parallelogram if opposite sides are equal.

 A quadrilateral is a parallelogram but not a rectangle if opposite sides are equal but the diagonals are not equal.

 A quadrilateral is a rhombus but not a square if all their sides are equal and the diagonals are not equal.

 

8. Circle:

         

The perpendicular from the center to a chord bisects the chord.

 There is one and only one circle passing through three non-collinear points.

 The angle in a semi-circle is a right angle.

 Opposite angles of a cyclic quadrilateral are supplementary.

 Angle in the same segment of a circle is equal.

 The tangent at any point of a circle is perpendicular to the radius through the point of contact.

 Two tangents to a circle from a point outside it are equal.

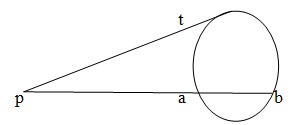
 If PT is a tangent to a circle and PAB is a secant, Then PA x PB= PT²