Easy Multiplication tricks for 2digit, 3digit and 4digit numbers
Multiplication is one of the trick for doing addition. The concept of multiplication is essentially that when we need to add a certain number consecutively.
For example add 24 eight times, i.e 24+24+24+24+24+24+24+24 so in this process of addition it is also do conveniently by using 24 x 8
In this article discussed about the easy method for doing the multiplication of 2 digit by 2 digit, 3digit by 3digit and 4digit by 4 digit numbers.
Friends
here having a simple algorithm in solution. Once you catch the logic
than it is very easy to remember. For your better understanding purpose I
wrote here in step by step. Once you can understand the steps you can
do solution in single step.
Multiplication of 2 digit number tricks :
In this process having 3 steps. for easy understanding purpose, here explained with alphabets as a number.
Take ab x cd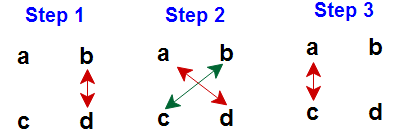 Let us go with one example 47 X 56
Let us go with one example 47 X 56
 Let us go with one example 47 X 56
Let us go with one example 47 X 56
Step 1 : ( b x d ) = 7 x 6 = 42. Take ” 2 ” for answer and “4” to be carry over to next step ( Ans : 2).
Step 2 : [ (a x d) + (b x c) ] + add number if any carry over from previous step
i.e [ (4 x 6) + (5 x 7) ] + 4 = 63. Take ” 3 ” for answer and “6” to be carry over to next step( Ans : 32)
Step 3 : ( a x c ) + add number if any carry over from previous step
i.e 4 x 5 =20 + 6 = 26 Take ” 26 ” ( Ans : 2632)
So final answer is 2632
Multiplication trick for 3 digit numbers :
In this process having 5steps. for easy understanding purpose, here explained with alphabets as a number. (abc x def)
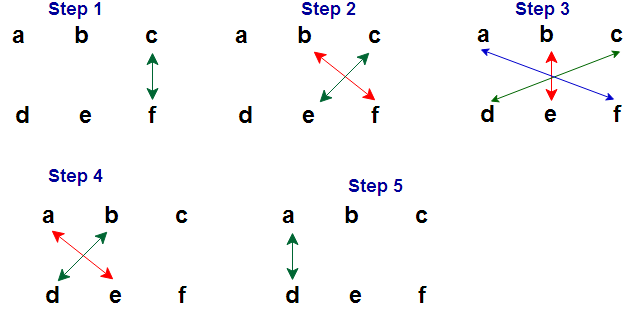
Now let us see one example 624 x 315

Step 1 : ( c x f ) = 4x 5= 20. Take ” 0 ” for answer and “2” to be carry over to next step ( Ans : 0)
Step 2 : [ (b x f) + (c x e) ] + add number if any carry over from previous step
i.e [ (2 x 5) + (4 x 1) ] + 2 = 16. Take ” 6 ” for answer and “1” to be carry over to next step( Ans : 60)
Step 3 : [ (a x f) + (b x e) + (c x d) ] + add number if any carry over from previous step
i.e [ (6 x 5) + (2 x 1) + (4 x 3) ] + 1 = 45. Take ” 5 ” for answer and “4” to be carry over to next step ( Ans : 560)
Step 4 : [ (a x e) + (b x d) ] + add number if any carry over from previous step
i.e [ (6 x 1) + (2 x 3) ] + 4 = 16. Take ” 6 ” for answer and “1” to be carry over to next step ( Ans : 6560)
Step 5 : ( a x d ) + add number if any carry over from previous step i.e ( 6 x 3) + 1 = 19 ( Ans : 196560)
So our final answer is 196560
Multiplication trick for 4 digit numbers :
In this multiplication process having 7 steps. for easy understanding purpose here explained with alphabets as a number. (abcd x efgh)
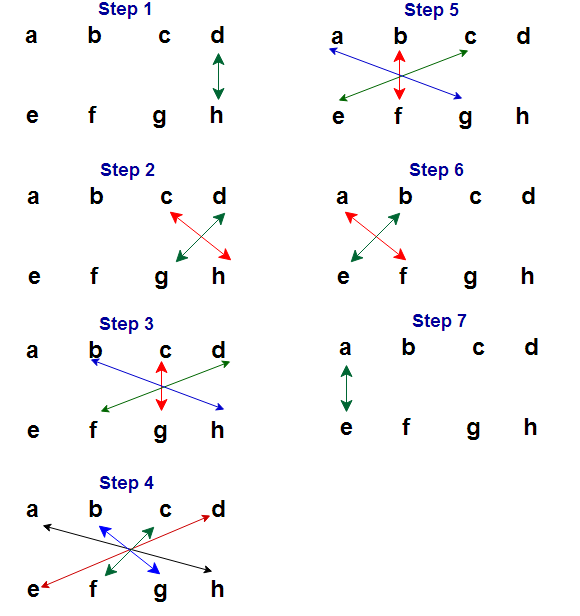
Now let us see one example 5243 x 7326

Step 1 : ( d x h ) = 3 x 6= 18. Take ” 8 ” for answer and “1” to be carry over to next step ( Ans : 8)
Step 2 : [ (c x h) + (d x g) ] + add number if any carry over from previous step
i.e [ (4 x 6) + (3 x 2) ] + 1 = 31. Take ” 1 ” for answer and “3” to be carry over to next step ( Ans : 18)
Step 3 : [ (b x h) + (c x g) + (d x f) ] + add number if any carry over from previous step
i.e [ (2 x 6) + (4 x 2) + (3 x 3) ] + 3 = 32. Take ” 2 ” for answer and “3” to be carry over to next step ( Ans : 218)
Step 4 : [ (a x h) + (b x g)+ (c x f) + (d x e)] + add number if any carry over from previous step.
i.e [ (5 x 6) + (2 x 2)+(4 x 3) + (3 x 7) ] + 3 = 70. Take ” 0 ” for answer and “7” to be carry over to next step ( Ans : 0218)
Step 5 : [ (a x g) + (b x f) + (c x e) ] + add number if any carry over from previous step
i.e [ (5 x 2) + (2 x 3) + (4 x 7) ] + 7 = 51. Take ” 1 ” for answer and “5” to be carry over to next step ( Ans : 10218)
Step 6 : [ (a x f) + (b x e) ] + add number if any carry over from previous step
i.e [ (5 x 3) + (2 x 7) ] + 5 = 34. Take ” 4 ” for answer and “3” to be carry over to next step( Ans : 410218).
Step 7 : ( a x e ) + add number if any carry over from previous step
i.e ( 5 x 7) + 3 = 38 ( Ans : 38410218)
So final answer is 38410218.
Multiplication tricks for easy calculations | Math Tricks
Multiplication of numbers plays very important role in math calculation. In this page explained some quick multiplication tricks to save time in math calculations. Depend upon the given numbers we chose the different types of multiplication tricks.
Type -1 : Multiplication tips for 2digit by 2 digit , 3digit by 3 digit and 4digit by 2 digit numbers. please go through the below link
Type -2 : The
given numbers are near to 10, 100, 1000 ( It can be solved in single
step by doing practice. Here for your understanding purpose given in
step by step)
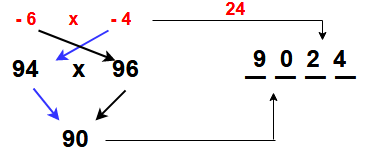
Example -1 : 94 x 96 = ?
Step-1: Find the value to roundup the given numbers i.e ( 94 + 6) & (96 + 4). i.e “-6” and “-4” ( Ans: _ _ _ _ )
Step-2: Multiplying the roundup numbers i.e – 6 x – 4 = 24 ( Ans: _ _ 24 )
Step-3: Add the roundup numbers for given numbers i.e (94 – 4 = 90) or ( 96 -6 = 90) ( Ans: 9024 )
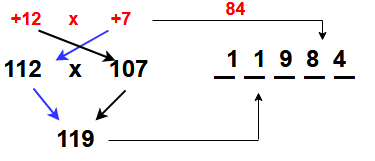
Example -2 : 112 x 107 = ?
Step-1: Find the value to roundup the given numbers i.e ( 112 – 12) & (107 – 7 ). i.e “+12” and “+7” ( Ans: _ _ _ _ _ )
Step-2: Multiplying the roundup numbers i.e 12 x 7=84 ( Ans: _ _ _ 84 )
Step-3: Add the roundup numbers for given numbers i.e (112+7 = 119 ) or ( 107+12 = 119) ( Ans: 11984 )
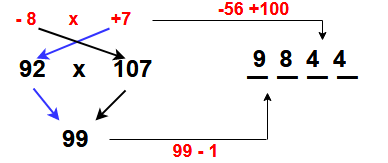
Example -3 : 92 x 107 = ?
Step-1: Find the value to roundup the given numbers i.e ( 92 +8) & (107 – 7 ). i.e “-8” and “+7” ( Ans: _ _ _ _ _ )
Step-2: Multiplying the roundup numbers i.e (-8) x (+7) = -56. So add 100 for this i.e -56+100 = 44 ( Ans: _ _ _ 44 )
Step-3: Add the roundup numbers for given numbers i.e (92+7 = 99 ) or (107-9 = 99). A gain subtract 1 from 99 i.e 99-1 = 98 ( Ans: 9844)
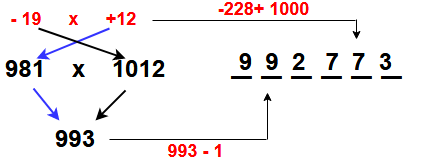
Example -4 : 981 x 1012 = ?
Step-1: Find the value to roundup the given numbers i.e ( 981+19) & (1012 – 12 ). i.e “-19” and “+12”
( Ans: _ _ _ _ _ _ )
Step-2: Multiplying the roundup numbers i.e (-19) x (+12 )= – 228. So add 1000 for this i.e -228+1000 = 772
( Ans: _ _ _ 772 )
Step-3:
Add the roundup numbers for given numbers i.e (981+12= 993 ) or
(1012-19 = 993). A gain subtract 1 from 993 i.e 993-1 = 992
( Ans: 992772)
The above sum 981 x 1012 = ? can be solved by using simple algebra formulas.
=981 x 1012 = 981 x (1000 + 12 )
=981000 + (981 x 12 )
Again 12 write as 10+2
= 981000+[ 981 x (10 + 2) ]
= 981000 + 9810 + 1962 = 992773
Type -3 : Multiplying the numbers by 5, 25 , 125.
Example -5 : 125468 x 5 = ?
Here using simple logic i.e replace 5 with ( 10 / 2 ). So add zero for given number and divide with 2.
125468 x 5 = 1254680 / 2 = 627340
Example -6 : 685624 x 25 = ?
Here using simple logic i.e replace 25 with ( 100 / 4 ). So add two zeroes for given number and divide by 4.
685624 x 25 = 68562400 / 4 = 17140600.
Example -7 : 3549 x 125 = ?
Here using simple logic i.e replace 125 with ( 1000 / 8 ). So add three zeroes for given number and divide by 8.
3549 x 125 = 3549000 / 8 = 443625.
Type -4 : Multiplying the numbers by 11, 22 , 33 …..88
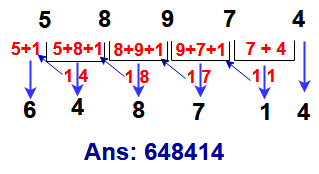
Example -8 : 58974 x 11 = ?
Here we can write answer in single step but for your understanding purpose given step by step
Step-1 : From 58974 take lost digit ( i.e 4 )and write in place of lost digit in your answer.
( Ans : _ _ _ _ _4)
Step-2 : From 58974 take lost and second digits and add it ( i.e 7 +4 = 11 ). Now take 1 and 1 carry over to next step.
( Ans : _ _ _ _ 14)
Step-3
: From 58974 take second , third digits and carry over number from lost
step and add it ( i.e 9 +7 + 1 = 17 ). Now take 7 and 1 carry over to
next step.
( Ans : _ _ _ 714).
Step-4
: From 58974 take fourth , third digits and carry over number from
lost step and add it ( i.e 8+ 9 + 1 = 18 ). Now take 8 and 1 carry over
to next step.
( Ans : _ _ 87 14).
Step-5
: From 58974 take first , fourth digits and carry over number from lost
step and add it ( i.e 5+ 8 + 1 = 14 ). Now take 4 and 1 carry over to
next step.
( Ans : _4 87 34).
Step-5
: From 58974 take first digit and carry over number from lost step and
add it ( i.e 1+5 = 6 ). Now take 6 into the answer.
( Ans : 64 87 34).
See the diagram for easy understanding.
Example -9: 2456 x 77 = ?
Here we can break down the numbers into simpler multiplication tasks. Now we apply above techniques.
i.e 2456 x 77 = 2456 x 11 x 7
= 27016 x 7 = 189112.
Type -5 : When sum of unit digit having 10 and remaining digits are same in the give problem.
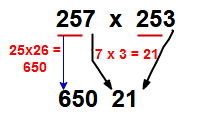
Example -10 : 257 x 253 = ?
Here sum of unit digits having 10 ( 7 + 3 = 10). and remaining digits are same in both. Now follow this technique
Step-1 : Multiply the lost digits i.e 7 x 3 = 21 ( Ans : _ _ _ 21)
Step-2 : Multiplying the remaining digits (same digits in both numbers) with preceding number i.e 25 x 26 = 650
Speed Math Division Shortcut tricks
Division shortcuts are very much helpful to save time in all our exams. As well as it will improve our analytical thinking. In this page we provided some examples of division shortcut methods.
Division process simply says as it is arithmetic operation of equal parts distribution of a number. If
we have 10pens and it is to be distribute equally to 5 persons then
each person get 2 pens (10/5 =2 ). So Division is the just inverse of the multiplication process.
First we know about some terminology like divided, divisor, Remainder, quotient in division math.
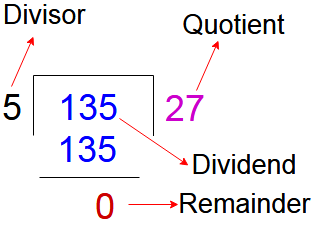
If percfect divisible numbers then we will write
- Dividend ÷ Divisor = Quotient.
- Quotient × Divisor = Dividend.
If remainder comes in division of numbers then we will write
- (Quotient × Divisor) + Remainder = Dividend.
Divisibility Rules of numbers from 1 to 20 given this below link
Now we discuss examples of shortcut division methods.
Method – 1 :
The dividend number in the given sum split as per our convenience. It
is purely depended upon the our analytical thinking ability.
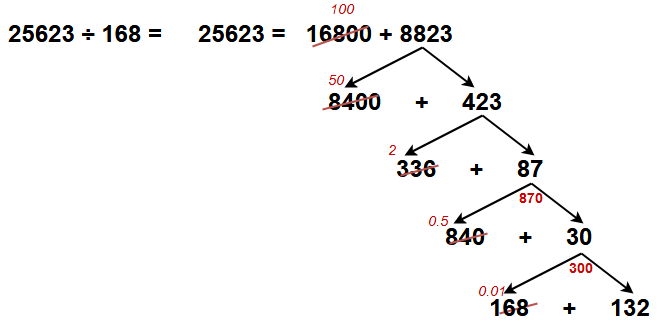
Example -1 : 25623 ÷ 168 = ?
First think about how to split the dividend in simple parts as per the given divisor.
Here i am splitting the dividend like 16800 + 8823. (Ans: 100+ — )
Now the number 8823 split as 8400 + 423. (Ans: 100+50+ — )
Again the number 423 split into 336 + 87. (Ans: 100+50+ 2+ — )
Now take decimal point and take the number 870 split as 840+ 30. (Ans: 152.51 _)
If you wont more accurate then go for next step.
Here provided diagram for better and easy understanding of division shortcut.
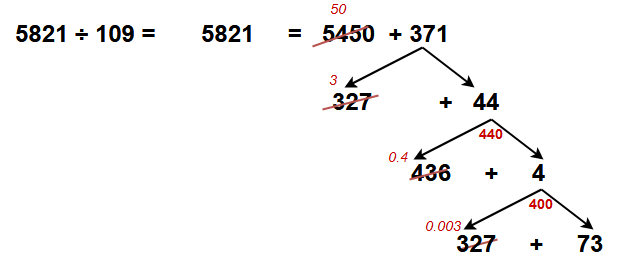
Example -2 : 5821 ÷ 109 = ?
Here i am splitting the dividend like 5450 + 371. (Ans: 50+ — )
Now the number 371 split into 327 + 44. (Ans: 100+3+ — )
Now take decimal point and take the number 440 split as 436+ 4. (Ans: 53.40 _)
If you wont more accurate then go for next step.
Example -3 : 82146 ÷ 24329= ?
If
given sum having five digits then cut the lost two digits from both
divisor and dividend. It will not effect much more on final answer.
Now calculate only for 821 ÷ 243.
I am splitting the dividend like 729 + 92. (Ans: 3+ — )
Now take decimal point and take the number 920 and split as 729+191. (Ans: 3+ 0.3 _)
Again take decimal point and take the number 1910 and split as 1701+209. (Ans: 3.3+0.07+ _)
If you wont more accurate then go for next step.
Method – 2 : Division trick for numbers 5, 25 and 125 in place of divisor.
Example – 4 : 269874 ÷ 5 = ?
Here we apply the simple logic i.e 5 = 10 / 2 . When compare to division by 5, it is very easy to multiplying the number by 2
i.e 269874 ÷ (10 ÷ 2) = (269874 x 2 ) ÷ 10 = 539748 ÷ 10 = 53974.8
Example – 5 : 5697823 ÷ 5 = ?
Now simple we doing the dividend multiplying by 2 and put decimal point before the lost digit of quotient.
i.e 5697823 x 2 = 11395646. Now put the decimal point before lost digit
So 5697823 ÷ 5 = 1139564.6.
Example – 6 : 56824 ÷ 25 = ?
Here
we apply the simple logic i.e 25 = 100 / 4. So simple we doing the
dividend multiplying by 4 and put decimal point before the lost two
digits of quotient.
i.e 56824 ÷ (100 ÷ 4) = ( 56824 x 4 ) ÷ 100 = 227296 ÷ 100 = 2272.96
Example – 7 : 23579 ÷ 125 = ?
Here
we apply the simple logic i.e 125 = 1000 / 8. So simple we doing the
dividend multiplying by 8 and put decimal point before the lost three
digits of quotient.
i.e 23579 x 8 = 188632. and put the decimal point before the lost three digits
So 23579 ÷ 125 = 188.632
Percentage formulas | percentage calculations with examples
Percentage calculation is one of the important part in mathematics. Percentage formulasvery helpful to all competitive exams as well as in our daily life. In this artical provides different types of formulas for percentage calculation with examples.
Type 1 : General Percent formulas.
Find X is what percent on Y ?
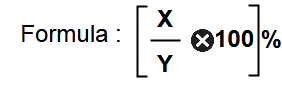
X is what percent greater than Y ?
Find X is what percent lesser than Y ?
Examples for the above percentage formulas
Ex. 1 : 25 is what percent on 40 ?
solution : (25/40) x 100 = 62.5%
Ex. 2 : 25 is what percent less than 40 ?
solution : [(40-25)/40] x 100 = 37.5%
Ex. 3 : 50 is what percent greater than 40 ?
solution : [(50-40)/40] x 100 = 25%
Type 2 : Net change of a number while percentage increase or decrease.
Net change of a number while increased by X% and then again increased by Y%.
Net change of a number while decreased by X% and then again decreased by Y%.
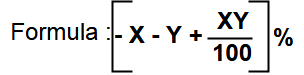
The Net change of a number while increased by X% and then again decreased by Y%.
Net change of a number while decreased by X% and then again increased by Y%.
Hints:
- Increase means ” + ” sign and decreased means ” – ” sign . If net change is positive, it means final value increased. If net change is negative, it means final value decreased.
- A number increases by x % and then again decreases by x %, (i.e same percent) then, net value always decreases by (x / 10)2
- If a number decreases by x % and then again increases by x %, (i.e same percent) then, net value always decreases by (x / 10)2
Examples for the above percentage formulas
Ex.1 : Find the net percent change of a number while it is increased by 20% and then again increased by 10% ?
Solution : 20 + 10 + ( 20 x 10 /100) = 32% increased.
Ex.2 : Find the net value of a number ” 60 “while it is increased by 25% and then again decreased by 15% ?
Solution : 25 – 15 – (25 x 15/100) = 25 – 15 – 3.75 = 6.25 % ( increased )
= 60 + (60 x 6.25 %) = 60 + [ 60 x (6.25/100)] = 60 + 3.75 = 63.75.
Ex.3 : Find the net value of a number ” 240 “while it is decreased by 30% and then again increased by 10% ?
Solution : -30 + 10 – (30 x 10/100) = – 30 + 10 – 3 = – 23 % ( decreased )
= 240 – (240 x 23 %) = 240 – [ 240 x (23/100)] = 240 – 55.2 = 184.8.
Ex.4 : Find the net percent change of a number while it is decreased by 20% and then again decreased by 30% ?
Solution : – 20 – 30 + ( 20 x 30 /100) = -20 – 30 + 6% = -44% (decreased).
Ex.5 : Find the net change in revenue, If price of a commodity decreases by 10% and again its price increases by 20%.
Solution : – 10 + 20 – (10 x 20/100) = -10 + 20 -2 = 8 %
The final price of the commodity increased by 8%.
Ex.6 : Find the net change in revenue, If price of a commodity decreases by 15% and again its price increases by 15%.
Solution : (15 / 10)2 = 2.25 %
The final price of the commodity decreased by 2.25%.
Type 3 : Net percent change in area of circle or square
If radius of a circle is increased by x%, then its area is increased by
If radius of a circle is decreased by x%, then its area is decreased by
Examples for the above percentage formulas
Ex.1 : Find the net change in area of a circle , If radius of the circle decreases by 20%and again its radius increases by 10%.
Solution : – 20 + 10 – [(20 x 10) / 100)] = -10 – 2 = -12% ( i.e radius decreased by 12% so change in radius 1- 0.12 = 0.88)
Area = π x r2 = π x (0.88 r)2 = 0.7744 x π x r2
So Area of the circle decreased by 100- 77.44 = 22.56%
Ex.2 : Find the net change in area of a circle , If radius of the circle increases by 30% and again decreases by 10%.
Solution : 30 – 10 – [(30 x 10) / 100)] = 20 – 3 = -17% ( i.e radius increased by 17% so change in radius 1+0.17 = 1.17)
Area = π x r2 = π x (1.17 r)2 = 1.3689 x π x r2
So Area of the circle increased by 136.89 – 100 = 36.89%
Ex.3 : Find the net change in area of a square , If side of the square increases by 30%.
Solution : (2 x 30) + (30 x 30 /100) = 60 + 9 = 69%
So Area of the square increased by 69%
Ex.4 : Find the net change in area of a circle , If radius of the circle decreases by 18%.
Solution : – (2 x 18) + (18 x 18 /100) = – 36 +3.24 = – 32.73%.
So Area of the circle increased by 32.73%.
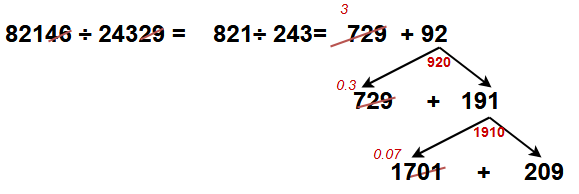
Comments
Post a Comment