SPEED MATH PART 2

 How to find the square of a two digit number easily

Square Means : When any number is multiplied by itself , it is called as the square of a number

a) Square plays very important role in mathematics.

b) For doing the square of any two digit number having number of shortcuts are there out of that I suggested you one of the best and easy trick for square

c) First of all I suggest you must remember squares of first 30 numbers. Upto 20 numbers most of the students already know so remaining number means upto 30, it is very easy to remember. It will also very much helpful to do square of 3 digit numbers.

d) After  30 you do not need to worry about that. You just following the process than you will able to do square of reaming 2 digit numbers.

Number	Square	Number	Square	Number	Square
1	1	11	121	21	441
2	4	12	144	22	484
3	9	13	169	23	529
4	16	14	196	24	576
5	25	15	225	25	625
6	36	16	256	26	676
7	49	17	289	27	729
8	64	18	324	28	784
9	81	19	361	29	841
10	100	20	400	30	900

Square of a number from 31 to 80 :

Here you must remember the following the  steps ( Note : Friends do not afraid for following steps it is very easy for better understanding purpose I mentioned here )

a) The answer having two parts and each part required for 2digits only. (except only for 31, here came one digit for 2nd part) .

b) Take number a “X” than  50 subtract from that number i.e X -50

c) For 1st part you square of that value i.e (X-50)2

d) In first part required 2 digits so if it came less than two digits than add “0” for second place otherwise if it came more than 2 digits than 3rd digit should be carryover the next part i.e 2nd part.

e) For Second part purpose our base number is 25. i.e the value X-50 is to be add to 25 and also to be add for this if any carry over number from 1st part.

Let us go through the examples.

Example No. 1 :   43²

Step 1 : 43-50 = -7

Step 2 : (-7)² = 49. Our 1st part 49.

Step 3 : 25+ (-7) + 0(No carry over from 1st part) = 18. Our 2nd part is 18.

So our final answer is 1849

Example No. 2 :   48²

Step 1 : 48-50 = -2

Step 2 : (-2)² = 4 Our 1st part 04 (Require 2digits in 1st part).

Step 3 : 25+ (-2) + 0(No carry over from 1st part) = 23. Our 2nd part is 23.

So our final answer is 2304

Example No.3 :   67²

Step 1 : 67-50 = +17

Step 2 : (17)² = 289 Our 1st part 89 (Require 2digits in 1st part and “2” carryover to 2nd part.).

Step 3 : 25+ (+17) + 2(it is carry over from 1st part) = 44. Our 2nd part is 44.

So our final answer is 4489

Square of a number from 81 to 99 :

Here you must remember the following the  steps

a) The answer having two parts and each part required for 2digits only.

b) Take number a “X” than  100 subtract from that number i.e X -100

c) For 1st part you square of that value i.e (X-100)2

d) In first part required 2 digits so if it came less than two digits than add “0” for second place otherwise if it came more than 2 digits than 3rd digit should be carryover the next part i.e 2nd part.

e) For Second part purpose our base number is X . i.e the value X-100 is to be add to X and also to be add for this if any carry over number from 1st part.

Example No.4 :   86²

Step 1 : 86-100 = -14

Step 2 : (-14)² = 196 Our 1st part is 96 (Require 2digits in 1st part so remaining value “1” is carryover to 2nd part.).

Step 3 : 86 + (-14) + 1(it is carry over from 1st part) = 73. Our 2nd part is 73.

So our final answer is 7396.

Example No.5 :   97 ²

Step 1 : 97-100 = -3

Step 2 : (-3)² = 9 Our 1st part is 09 (Require 2digits in 1st part).

Step 3 : 97 + (-3) + 0(it is carry over from 1st part) = 94. Our 2nd part is 94.

So our final answer is 9409.

Friends definitely I can tell while you are doing the practice the above shortcut way than you can definitely do square of two digit number in fraction of section.

Friends in this blog explained about easy methods for all types of mathematics sums

 Easy methods for Cube of a Number | cube of a number calculator

Cube of a number means , If any number is multiplied by itself three times, then the product is called the cube of that number.

Generally the cube of a number denoted as, 3 is written a little up to the right of the numbers.

Here Discussed different easy methods to find the cube of a number without calculator. It will help to all students to do fast calculation in there regular and commutative exams.

First remember cube of a number from 1 to 10. 

( 1³= 1 ;

2³= 8 ;

3³= 27 ;

4³= 64 ;

5³= 125 ;

6³= 216 ;

7³= 343 ;

8³= 512 ;

9³= 729 ;

10³= 1000 )

As per the given number we can choose the method for cube of that number

Method : 1 (Cube of a Number End with Zero )

Ex. 1 : Find the cube of  70 ( 70³= ? )

Simple we can write the value of  7³  and add three zeros in right side. i.e 7³  = 343  and  70³ = 343000

Method : 2 ( Cube of a number just near to ten place)

Ex. 1 : Find the cube of 11 ( 11³= ? )

Use the simple algebra formula  (a + b)³ = a³ + 3a²b + 3ab² + b³. 

we can write 11³  = ( 10 + 1 )³ . So here take a = 10 , b = 1 then

( 10 + 1 )³ = 1000 + 300 + 30 + 1 = 1331.

Ex. 2 : Find the cube of 48 ( 48³= ? )

Use the simple algebra formula  (a – b)³ = a³ – 3a²b + 3ab² – b³. 

we can write 48³  = (50- 2 )³ . So here take a = 50 , b = 2 then

( 50 – 2 )³ = 125000 – 15000 + 600 – 8 = 110592.

Method : 3 (Cube of  two digit number).

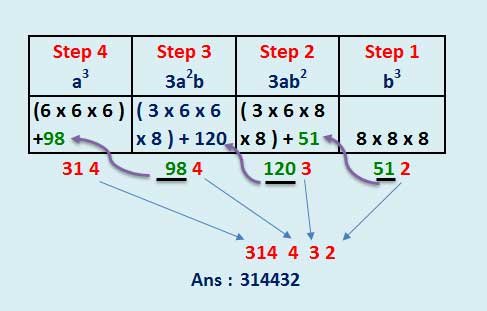
Ex. 1 : Find the cube of  68 ( 68³= ? )

Take formula (a + b)³ = a³ + 3a²b + 3ab² + b³.  and here assume  Here, a = 6 and b =8.

Step 1 : Take b³ = 8 x 8 x 8 = 512. Take lost digit into the answer last place and remaining value to be add to next step.

i.e Ans :  _ _ _ _ _ 2  and 51 to be add in the next step.

Step 2 : Take 3ab² = 3  x 6 x 64 =  3 x 384 = 1152 and 51 ( from previous step). So 1152 + 51 = 1203. Here Take lost digit into the answer next place and remaining value to be add to next step.

i.e Ans :  _ _ _ _ 3 2  and 120 is to be add in the next step.

Step 3 : Take 3a²b =(3  x 36 x 8) + 120=  864 + 120 = 984.  Here Take lost digit into the answer next place and remaining value to be add to next step.

i.e Ans :  _ _ _43 2  and  98 is to be add in the next step.

Step 4 : Take a² =(6 x 6 x 6) + 98=  216 + 98 = 314.  Take this  value into the answer next places.

i.e  Ans : 31443 2.

Therefore, (68)³ = 314432.

Method : 4 ( Cube of any number).

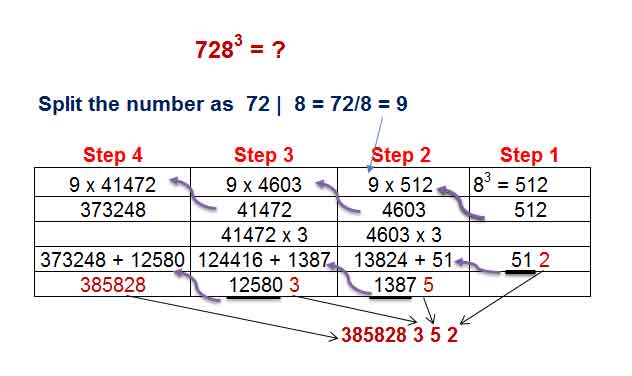
Ex. 1 : Find the cube of  728 ( 728³= ? )

Step 1 : Split the number as like i.e  7 – 28 or 72 – 8.

Here we take 72 – 8 .

Step 2 : Divide the 1st part by 2nd part. i.e 72/8 = 9. Here we can take a = 8 , b= 9 , c = 8³ = 512

Step 3 : Cube of 1st part c = 8 x 8  x 8 = 512. Here Take last digit in answer and remaining value 51 to be add to next step.

i.e Ans :  _ _ _ _ 2  and 51 is to be add in the next step.

Step 4 : 3 bc + 51= (3 x 9 x 512) +51=  13824 + 51 = 13875 . Here Take lost digit into the next digit in answer and remaining value 1387 to be add to next step.

i.e Ans :  _ _ _ 5 2  and 1387 is to be add in the next step.

Step 5 : 3 b² c +13875= (3 x 9 x 9 x 512) +1387= 124416 + 1387 = 125803 . Here Take lost digit into the next digit in answer and remaining value 12580 to be add to next step.

i.e Ans :  _ _ _3 5 2  and  12580 is to be add in the next step.

Step 6 : b³ c +12580= ( 9 x 9 x 9 x512) +12580= 373248 + 12580 = 385828. Here Take this value into the answer

i.e Ans :  385828352.

Square Root calculation methods | square root formulas

Definition of square root : Mathematically, it is defined as ”  square root of a number is a value that, when multiplied by itself, gives the number”. i.e When a number is multiplied by itself to give the square of number then that number is a square root for that square number. Square root represented by a the symbol ” √ ”

Now here we learn different methods for finding the square root

a) Square Root of a any number by the long division method. (It is general method for square root calculation).

b) Square Root of a Perfect Square by using the Prime Factorization Method.

c) Short cut trick for find the square root for perfect square number.

d) Approximate Square Root of any number which is not a Perfect square.

Square Root of a any number by the long division method.

Here explain with example in step by step.

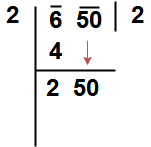
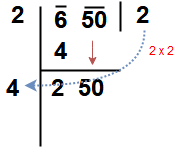
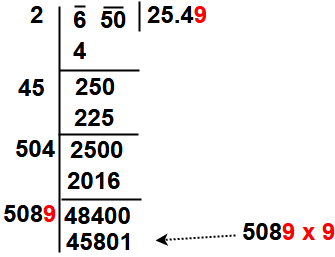
Take a example Find √650 to one decimal place.

Step 1 : The given number to be group the digits in pairs, and the remaining digit (if any) is called a period.

Here our given number 650. So it is group as 6 – 50

Step 2 : Find the largest number whose square is equal to or just less than the first period or pair.   Here Square the 2, giving 4, and Square the 3, giving 9. So write 4 that underneath the 6. Take the number ‘ 2 ” as the divisor and also as the quotient.

Step 3 : Now take Subtract the product of the divisor and the quotient  (i.e 2 x 2 = 4) from the first period or pair ( i.e 4). Bring down the next pair of digits and this becomes the new dividend.

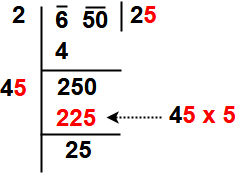
Step 4: Now, the new divisor is obtained by taking two times the quotient. Here quotient is 2 so new divisor 2 x 2 = 4 and the new dividend is 250.

Step 5: Now think suitable single digit number which is also taken as the next digit of the quotient. The single digit is to be choose like the product of  that product of the new divisor and the this single digit to be equal to or just less than the new dividend.

Here check one by one digit i.e 41 x 1 = 41 , 42 x 2 = 84, 43 x 3 = 129, 44 x 4 = 176, 45 x 5 = 225, 46 x 6 = 275 . So take the single digit is 5.

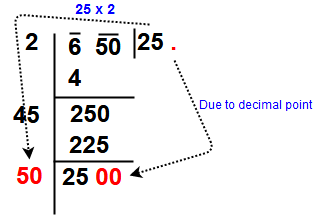
Step 6 :  Subtract and bring down the next pair of digits to dividend. So here not having the pairs so put the decimal in quotient place and drop down digits 00. The new divisor is obtained by taking two times the quotient. Here quotient is 25 so new divisor 2 x 25= 50 and the new dividend is 2500.

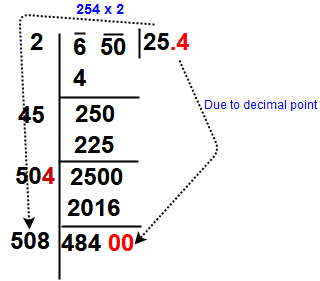
Now Repeat steps (4), (5)and (6)  till all the periods have been taken up. Finally the quotient so obtained is the required square root of the given number.

So our final answer is √650 =  25.49 = 25.5.

Square Root of a Perfect Square by using the Prime Factorization Method.

This method applicable only the for the perfect square root numbers

Step1 : Write given number into prime factors.
Step2 : Make pairs of similar factors.
Step 3 : Take the product of prime factors, then choosing one factor out of each pair.

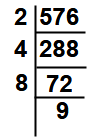
Example : Find the Square root of 576 by prime factorization method.

Factors of 576 = 2 x 4 x 8 x 9

Prime Factors of 576 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

Collect the one factor out of each pair i.e = 2 x 2 x 2 x 3 = 24

So √576 = 24.

Short cut trick for find the square root for perfect square number.

This method applicable only the for the perfect square root numbers

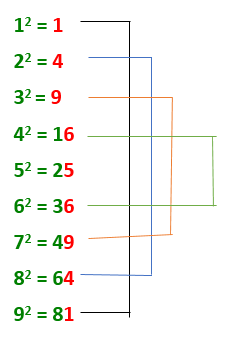
Remember the following table ( i,e squares of 1 to 9 numbers) and given simple logic.

• • If last digit of perfect Square number =1, last digit of Square root for that number=1 or 9.
  • If last digit of perfect Square number =4 , last digit of Square root for that number=2 or 8.
  • If last digit of perfect Square number =9, last digit of Square root for that number=3 or 7.
  • If last digit of perfect Square number =6, last digit of Square root for that number=4 or 6.
  • If last digit of perfect Square number =5, last digit of Square root for that number=5.

Take example

Ex. 1: Find the square root of  7056.

Step 1 : The given number to be group the digits in pairs, and the remaining digit (if any) is called a period. Write two digit  parts  i.e  70 – 56  and Lost digit is ” 6 ” so last digit of Square root for that number=4 or 6.

Step 2 : Leave the first two digits and take the next remaining digits. Here remaining number is ” 70″.

Step 3 : Find the less square number for ” 70″ .

i.e 8² < 70 < 9²

So Take the less number i.e ” 8″ . Here our next digit of square root is ” 8 “

Step 4 : Square root of  7056 is 84 or 86.

Step 5 : Take the second digit in square root (i.e 8 ) and multiplying it, by next preceding number (i.e 8 x 9 = 72 ).

Step 6 :  Compare the multiplied value ( i.e 72) with the 2nd part of the number  (i.e 70 ).

If the 2nd part of the number is high then take big number.

If the 2nd part of the number is less then take small number.

Here ( 2nd part of the number)  70 < 72 . So take small number 84 from  84 and 86.

Square root of 7056 is  86.

Ex. 2 : Find the square root of  784

Step 1 : Separate the number into two digits (i. e 7 – 84) and Identify the lost digit of the number. Here lost digit is ” 4″ so last digit of Square root for that number=2 or 8.

Step 2 : Leave the first two digits and take the next remaining digits. Here remaining the number is ” 7″.

Step 3 : Find the less square number for ” 7″ .

i.e 2² < 7 < 3²

So Take the less number i.e ” 2″ . Here our next digit of square root is ” 2 “

Step 4 : Square root of 784 is 22 or 28.

Step 5 : Take the second digit in square root (i.e 2 ) and multiply it by next preceding number (i.e 2 x 3 = 6 ).

Step 6 : Compare the multiplied value ( i.e 6) with the 2nd par of the number (i.e 7 )

Here 7 > 6 . So take height number 28 from  22 and 28.

Square root of 784 is  28.

Approximate Square Root of any number which is not a Perfect square.

Formula in this method :

Square Root of the number = Square Root of Nearest Perfect Square + { [ difference of the given number from the nearest perfect square] / [ 2  x Square root of Nearest Perfect Square]

For example,

Find the Square Root of  650.
Sol :perfect square closest to 625 is 25; we will take square root of 625 i.e. 25 in this calculations
= 25 +[ (650-625) / (2 x 25) ]
= 25 + [  25 /( 2×25)]
=25 + 0.5
= 25.5 (approximate value).

Find the Square Root of  1009.
perfect square closest to 1009 is 32; we will take square root of 1024 i.e. 32 in this calculations
= 32 – [ (1024-1009) / (2 x 32) ]
= 32 – [  15 /( 2×32)]
=32 – 0.23 = 31.77 (approximate value).

How to find cube root of a number quickly | Cube Root Calculator

The cube root of a number means it is a value of that, when used in a multiplication by itself in three times, gives that number.

In this page explained about one simple and easy tip for finding Cube Roots of Perfect Cubes  of two digits numbers. By this cube root formula we find cube root in fraction of seconds.

These points to be remember for this cube root formula.

1. 1. The given number should be perfect two digit cube.
   2. Remember cubes of 1 to 10 numbers.
   3. As per the cubes identify as follow as below table.

13 = 1	If last digit of perfect cube number =1, last digit of cube root for that number=1
23 = 8	If last digit of perfect cube number =8, last digit of cube root for that number=2
33 = 27	If last digit of perfect cube number =7, last digit of cube root for that number=3
43 = 64	If last digit of perfect cube number =4, last digit of cube root for that number=4
53 = 125	If last digit of perfect cube number =5, last digit of cube root for that number=5
63 = 216	If last digit of perfect cube number =6, last digit of cube root for that number=6
73 = 343	If last digit of perfect cube number =3, last digit of cube root for that number=7
83 =512	If last digit of perfect cube number =2, last digit of cube root for that number=8
93 = 729	If last digit of perfect cube number =9, last digit of cube root for that number=9
103 = 1000	If last digit of perfect cube number =0, last digit of cube root for that number=0

If we put interest on mathematics then it is a very interesting subject and easy to learn. Now let’s see how we can easily find out cube roots of perfect cubes with in fraction of seconds.

Take examples to easily understand the cube root formula

Example 1: Find Cube Root of 13824

Step 1

Identify the last three digits from right side and make group of these three digits

i.e., 13 – 824

Step 2

Take the last group which is 824. And then find the last digit of 824 is 4

According to above table if last digit having 4 then last digit of cube root for that number is 4

Hence the right most digit of the cube root of the given number is 4

Step 3

Take the next group which is 13

Find out the value of 13 lies in between the cube of the numbers 2³ and 3³

8 < 13 < 27

Take small cube number i.e “ 2 “

Hence the left neighbor digit of the answer is 2

So our answer = 24

Example 2: Find Cube Root of 175616

Step 1

Identify the last three digits from right side and make group of these three digits

i.e., 176 – 616

Step 2

Take the last group which is 616. And then find the last digit of 616 is 6

Square root multiplication modal:
In this there are two models fineta and infinet modal
Formula for finite modal is

Whare P is  

For example:

√6√6√6√  6
Here A=6
P=      is         n=4  number of roots
The final ans is

 
For infinite model
 √6√6√6√  6
Answer is A
Then the answer is 6


Square root infinet subtraction and addition:
√20+√20+√20+√ 20___
For  these cases would general to give number of the form giben below
a*(a+1)
20=4(4+1)+4*5
For addition the bigger value is considered that is 5
For subtraction smaller value in considered that is 4